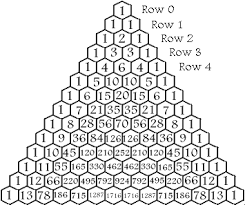
A very important concept in mathematics is the Pascal’s Triangle. What is it? Well here it is:

The Pascal’s Triangle begins with 1, followed by the next row, which consists of 2 ones and then 121. Notice that there are 1’s on each side and notice in Row 2 that 1+1 is 2, as shown above, the two, there are two ones. You can actually pick a random number, let’s say 10 on Row 5. You can obviously see that each 10 is equal to 6+4, and here’s a quick fact: the digits of all of these rows are powers of 11. Actually, you can do 11^4 on the calculator and get 14641. For 11^n, the value of that will be equal to each digit corresponding to Row #n. That may be confusing, but it’s actually not.
Now, another concept that is formed by the Pascal Triangle is expanding the sum of (a+b). If you know from Algebra I and II, (a+b)2 is a2+2ab+b2 , and (a+b)3 is a3+3a2b+3ab2+b3 . The coefficients of the first pattern in order is 121 since it is equivalent to 1a2 +2ab+1b2 . And in the other one, it is 1331. See, we can make a conclusion: for every (a+b)n then the order of the coefficients for the expression will be the numbers for the nth row. That means we can solve for any of the (a+b)n expressions. Now, I’ve solved (a+b)10 for you, and you can solve it on your own, too. The only thing that can be tricky for some people is the A’s and the b’s on each term. Let’s first start by saying the coefficients are question marks. The terms go like this:
?a10b0 + ?a9b1 + ?a8b2 + ?a7b3
+ ?a6b4 + ?a5b5 + ?a4b6 + ?a3b7 + ?a2b8 + ?a1b9 + ?a0b10 .
Notice that for each term, the powers of the a and b add up to 10, which is our power index in the first place. So when solving (a+b)n the index power for the second term will always be n-1, and it continues subtracting one while the other term increases. In addition, the index powers always add up to n. For each (a+b)n there are n+1 terms in the expanded version. And for the ? marks, you fill the numbers in the Pascal’s triangle(in row 10) and you are done!!! Hopefully you learned something today, and here is my work down below: