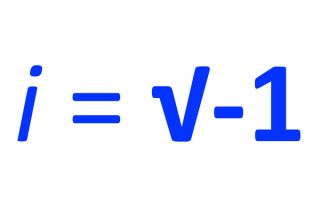Intro. to Imaginary Numbers

(for very experienced Algebra I students / Algebra II)

Inventions, as always in history weren’t always appreciated by humans. However, many inventions led to a whole new idea that impacted history forever. For example, Leonhard Euler’s invention of the complex number $i$ .

You might be wondering what number’s square is negative. For example, find the value of $x$ such that $x^2 = -1$ . Well, you could think that there are no solutions. Any negative squared is positive. A positive squared is positive. Zero squared is zero. No solutions.

But as mentioned already, there is a notation for denoting these kinds of numbers, and the set of these numbers are called imaginary numbers. The definition of the number $i$ is that $i^2 = -1$. So you could say that $i = \sqrt{-1}$ , where we denote $i$ as the imaginary unit.

Let’s do some arithmetic with these types of numbers.

Addition and subtraction would just be the same as a variable. If you add $2x$ and $3x$ , you would get $5x$ . We can use the same “adding coefficients rule” for this: $2i + 3i = \boxed{5i}$ . You could do the same with the subtraction method.

Multiplication and division are a little different with this “i”. Let’s see what happens when you raise $i$ to some integer powers. (I might talk about fractional powers later)

$i^1 = i$
$i^2 = i \cdot i = -1$
$i^3 = i \cdot i^2 = i \cdot -1 = -i$
$i^4 = i \cdot -i = -(i^2) = 1$

We can immediately see that after $i^4$ , the pattern repeats since the next power of $i$ after 4 would be $1 \cdot i = i$ .

We conclude our observations: the powers of $i$ rotate in blocks of four: i, -1, -i, 1.

How does this have to do with multiplication and division? Well a lot, actually.

Let’s start with multiplication. For starters, multiply $8i \cdot 9i$ . We can denote this as $72i^2$ , so the answer would be $-72$ , since $i^2 = -1$ .

You simply add the powers of $i$ , divide the sum by four using the standard division algorithm, and use our rotating “i” pattern. Here’s what I mean:

Example: Evaluate $61i^{6}(7i^{12})$ . (try it out on your own before resorting to the solution)